📚 Click/Tap Here
Visual Clues
1. What
season is it?
A. winter
B. summer
2. When is
it?
A. noon
B. midnight
C. morning or evening
3. Why do
the trees look that way?
A. The trees
are dying.
B. A
storm covered them with ice and snow.
C. They are blooming.
4. How would
your footsteps sound if you were to walk on the ground?
A. squish
B. slurp
C. crunch
5. What
might live nearby?
A. a wild
moose
B. a wild
giraffe
C. a wild alligator
Statistical Data
Statistical data is information collected in the form of numbers or categories. It helps us understand things by looking at patterns and trends.
For example, if we collect data on how many students like different subjects, we can see which subject is the most popular.
Exercise:
1. If marks obtained by students in a class test is given as per below:
55 36 95 73 60 42 25 78 75 62
Then arrange the marks from lowest to highest.
Solution:
25 36 42 55 60 62 73 75 78 95
2. Check the following frequency distribution table, consisting of weights of 38 students of a class:
(i) What is class-interval for classes 31 – 35?
(ii) How many students are there in the range of 41-45 kgs?
Solution:
(i) Class interval = Upper class limit – lower class limit
= 35-31
= 4
(ii) For the 41-45 range, there are 14 students.
Definitions
3. A family with a monthly income of 20,000 had planned the following expenditures per month under various heads:
Draw a bar graph for the data above.
Solution:
Bar Graphs
A bar graph is a chart that uses bars (rectangles) to show different amounts or numbers. The taller the bar, the bigger the number. It helps compare things easily, like the number of students in different classes.
Exercise:
1. The table below shows the favourite colour of 200 kids in a class.
(1) Using the information provided, create a bar graph.
(2) Which colour is the most preferred and which colour is the least preferred?
(3) How many kids chose red as their favourite colour?
Solution:
(2) Blue is the most preferred colour and green is the least preferred colour.
(3) 45 students.
Pie Charts
A pie chart is a circle divided into slices, like a pizza, to show parts of a whole. Each slice represents a portion of the total.
For example, a pie chart can show how a family's budget is spent on food, rent, and other things.
Exercise:
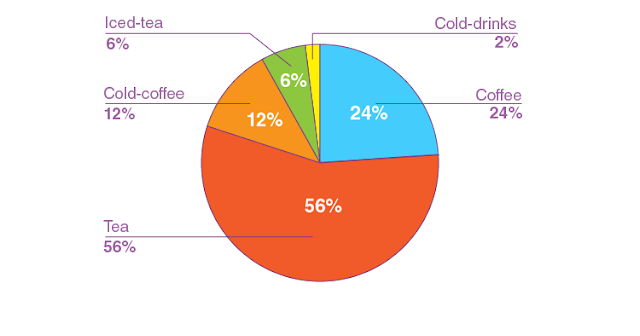
In the summer, a survey was conducted among 400 people about their favourite beverages. The following pie chart shows the data:
Answer the following questions:
(i) How many people like tea?
(ii) How many more people like coffee than cold coffee?
Solution:
(i) Total number of people = 400
Number of people like tea = 400 × 56/100 = 224
(ii) Number of people like coffee = 400 × 24/100 = 96
Number of people like cold-coffee = 400 × 12 = 48
Number of people like coffee more than cold-coffee = 96 – 48 = 48.
Histograms
A histogram looks like a bar graph but is used to show how often something happens in a range. The bars touch each other, showing that the data is continuous.
For example, a histogram can show how many students scored within certain marks in a test (0-10, 11-20, etc.).
Exercise:
Question 1:
The below histogram shows the weekly wages of workers at a construction site:
Answer the following questions:
(i) How many workers get wages of ₹ 60-70?
(ii) Construct a frequency distribution table.
(iii) What is the cumulative frequency for the class 50-60?
Solution:
(i) 16 workers
(ii)
(iii) The cumulative frequency for the class 50-60 = 10 + 20 + 40 = 70.
style="background-color: white;">Question 2:
Study the given histogram:
Answer the following questions:
(i) Prepare a cumulative frequency distribution table for the above histogram.
(ii) Which class interval has the maximum frequency?
(iii) Which class interval has the minimum frequency?
Solution:
(i)
(ii) 10-20 class interval.
(ii) 30-40 class interval.
Cumulative Frequency
Cumulative frequency is the total of a frequency added up as you go. It shows how many values are at or below a certain point in a dataset.
Suppose a teacher records the number of students scoring within different marks in a test:
| Marks Range | Number of Students (Frequency) | Cumulative Frequency |
|---|---|---|
| 0 - 10 | 3 | 3 |
| 11 - 20 | 5 | 3 + 5 = 8 |
| 21 - 30 | 7 | 8 + 7 = 15 |
| 31 - 40 | 4 | 15 + 4 = 19 |
- The first cumulative frequency is 3 (only the first group).
- The second is 8 (adding 3 + 5).
- The third is 15 (adding 8 + 7), and so on.
Cumulative frequency helps to find medians, quartiles, and trends in data.
Median
The median is the middle value in a set of numbers when arranged in order. If there are two middle numbers, the median is their average.
Example:
In the numbers 3, 5, 7, 9, 11, the median is 7 because it is in the middle.
If the numbers are 2, 4, 6, 8, the median is (4+6) ÷ 2 = 5.
Quartiles
Quartiles divide a set of numbers into four equal parts to help understand how the data is spread.
Steps to Find Quartiles:
- Arrange the numbers in order (smallest to largest).
- Find Q2 (Median) – This is the middle number.
- Find Q1 (First Quartile) – The middle of the lower half (left side).
- Find Q3 (Third Quartile) – The middle of the upper half (right side).
Example:
Suppose we have this data:
2, 4, 6, 8, 10, 12, 14, 16, 18
The middle number is 10 (because it is in the center).
Find Q1 (First Quartile - Q1):
The lower half: 2, 4, 6, 8
The middle of this part is 5 (average of 4 and 6 → (4+6) ÷ 2 = 5).
The upper half: 12, 14, 16, 18
Final Quartiles:
Q1 = 5
Q2 (Median) = 10
Q3 = 15 style="background-color: white;">
So, quartiles help us understand how data is distributed by dividing it into four equal sections.
Trends
A trend shows a pattern or direction in data over time. It helps predict future outcomes.
- Example: If sales increase every month (100, 120, 150, 180), there is an upward trend. If they decrease (200, 180, 160, 140), there is a downward trend.